Derivatives of Power
Functions
and Polynomials.
If f(x) = xn then f '(x) = nxn-1
Polynomials are sums of power functions. In order to obtain their derivatives,
we need to establish the following facts:
![]()
where c is independent of x, and
![]()
While these rules are being applied to power functions and polynomials first, they work for any functions.
Examples:
1. A polynomial with positive and negative exponents.
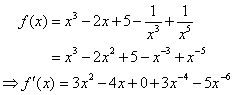
In this example, we rewrote the rational terms as power terms with negative exponents.
2. A rational function with a single term in the denominator.
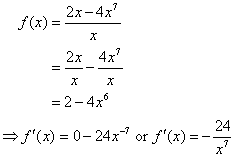
In this example, we split the fraction and simplified before taking the derivative. This is often simpler than employing the quotient rule.
3. A function with a radical term.
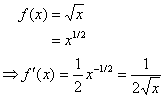
In this example, we rewrote the radical in terms of a rational exponent. The last result is what we obtain when we find the derivative using the definition of the derivative.
4. Another function with more complex radical terms.
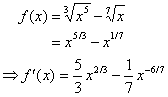
Derivatives of
Exponential Functions.
![]()
Examples:
1. The derivative of 2 x.
![]()
2. The derivative of 5(4.6)x.
![]()
3. The derivative of (ln3)x.
![]()
4. The derivative of e x.
![]()
This last result is the consequence of the fact that ln e = 1.
When a function is the product of two functions, or can be deconvolved
as such a product, then the following theorem allows us to find its derivative:
If y = f(x)g(x), then [f(x)g(x)]’ = f’(x) g(x) + f(x) g’(x)
Another way to write this, using Leibniz' notation is
![]()
Notice that the derivative of a product of functions is not just the product of their derivatives; the derivative is somewhat more complex. That is,
![]()
Instead, we have
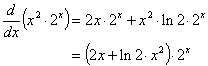
Examples:
1. The product f(x) = (2x + 1)(x2 - 2).
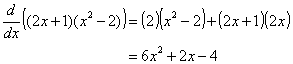
You should verify that if you had FOILed the product first, then taken the derivative, the result would have been the same.
2. Another example:
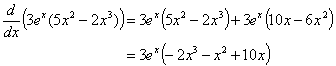
Factoring the result at the end is usually convenient for algebraically finding critical points and intervals of increase/decrease.
3. An example of numerically defined functions. Let f(2) = 1, f '(2) = -1, g(2) = -3, and g'(2) = 4. Find the derivative of f(x)g(x) at x = 2.
Solution: By the product rule, the derivative of the product of f and g at x = 2 is
f '(2)g(2) + f(2)g'(2) = (-1)(-3) + (1)(4) = 7
When a function is the quotient of two functions, or can
be deconvolved as such a quotient, then the following theorem allows us to find
its derivative:
If y = f(x)/g(x),
![]()
Another way to write this, using Leibniz' notation is
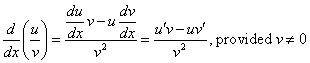
Notice that the derivative of a quotient of functions is not just the quotient of their derivatives; the derivative is somewhat more complex. That is,
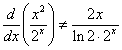
Instead, we have
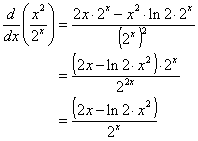
Examples:
1. A rational function of polynomials:
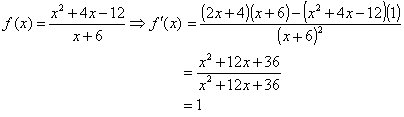
You should verify that this is the result we would obtain if we had algebraically simplified the rational function first, then taken the derivative.
2. Another rational function which cannot be algebraically simplified:
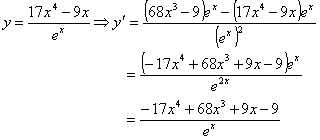
3. An example of numerically defined functions. Let f(2) = 1, f '(2) = -1, g(2) = -3, and g'(2) = 4. Find the derivative of f(x)/g(x) at x = 2.
Solution: By the quotient rule, the derivative of the product of f and g at x = 2 is
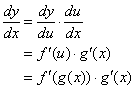
This is the chain rule. It requires these steps:
· For a composite function, write f as a function of u, and u itself a function of x.
· Find the derivatives of f and u.
· Apply the chain rule to find the derivative of the composite function.
It is convenient and easy to think of composed functions as an "outside" function and and "inside" function. We take the derivative of the outside function, leaving the inside function alone. This is the f '(g(x)) part. Then we multiply the result by the derivative of the inside function. This is the g'(x) part.
Notice that the derivative of composed functions is not merely the composed derivatives:
![]()
Rather,
![]()
Here, ex is the "outside function" and x2 is the "inside" function.
Examples:
1. A polynomial to a power.
![]()
2. If f(x) = e x and g(x) = x 2 + 3x, find f(g(x)) and f (g(x))¢.
Solution:
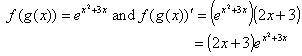
3. An example of numerically defined functions: If f(2) = 5, f¢ (2) = -1, g(1) = 2, and g¢ (1) = 4, find f (g(1)) and f (g(1))¢.
Solution using the meaning of composed functions, the chain rule and the given data:
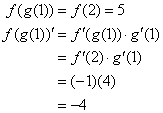
4. The hot glowing gas of a star radiates energy according to the function E = sT 4.If T is a function of the radius of the star, use the Chain Rule to find a formula for dE/dr.
Solution, using the chain rule:
In this case, we do not have an expression for dT/dr, so we leave the derivative of T alone. We encounter this type of situation often when solving related rates problems. This reveals that E is really an implicit function of r, that is, it depends on r, but the manner in which it depends on r may not be obvious, or explicit.
The definition of the derivative and the addition formulas for sine and cosine can be used to derive the following theorems:
![]()
Similarly, the following derivatives can be derived:
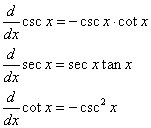
Examples.
1. Find the derivative of y = 2sin x + 3tan x.
Solution: Using the above theorems, y' = 2cos x + 3sec2 x
2. A population of foxes varies seasonally according to the model
![]()
where P is in thousands and t is in months since Jan 1. Find a function that models the rate of change of the fox population with respect to time.
Solution: Using the above theorem for the derivative of cosine and the chain rule:
3. Show that the functional side of the Pythagorean Identity is indeed constant for all x.
Solution: the Pythagorean Identity is sin2x + cos2x = 1. Taking the derivative of the left side of the equation gives us:
2sinxcosx + 2cosx(-sinx) = 2sinxcosx - 2sinxcosx = 0
Since the derivative equals zero, the rate of change is zero (for all x), hence the identity is a constant.
The derivatives of various other functions can be obtained by the chain rule and the composition of inverse functions. The method goes like this:
Suppose f(x) is differentiable and its inverse function f -1(x) is also differentiable. When they are composed, the result is
f -1(f(x)) = x.
To find the derivative of f(x), the derivative of the composed functions, obtained via the chain rule, yields the following result:
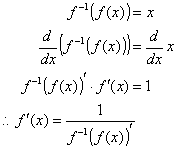
Suppose f(x) = ln x. Then f -1(x) = e x. Then f -1(f (x))’ = e ln x = x. Thus, the following:
![]()
Other derivatives obtainable by this method include:
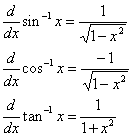
The hyperbolic functions are defined as
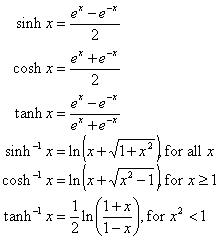
Their derivatives are obtainable by the rules outlined above:
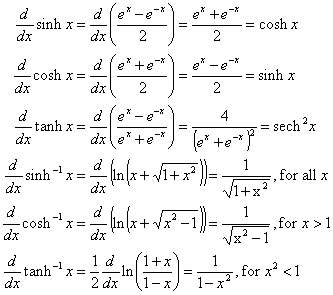
Parametric equations describe the motion of a point P as independent functions of the parameter t as it wanders about the xy-plane. The x- and y-coordinates are
x f(t) and y = g(t)
Parametric curves come in mind-boggling variety. Any choice of two such equations and a t-interval produces a parametric curve. Often the result is beautiful, useful, interesting, or all three.
The rate of change of position, P = (f(t), g(t)) along a parametrically defined curve is given by
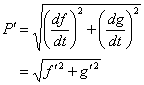
This is often thought of as the velocity of the particle since for many applications the independent variable t represents time. The slope of the parametric curve is given by
![]()
The location of a point on the xy-plane can be expressed in polar form, that is, in terms of its distance (radius, r) from the origin and the angle, q, its radius vector makes with the positive x-axis. Cartesian (rectangular) graphs are often represented y = f(x). Such functions can also be represented in polar form r = f(q). Conversion of points or equations between systems are via the transformation equations:
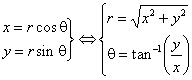
The derivatives of x and y with respect to q are obtainable by the product rule:
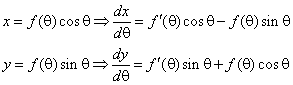
Thus the slope of a polar curve is given by
![]()
Vectors are quantities that have both magnitude and direction. For a vector of the form
![]()
its magnitude is
![]()
and its direction with respect to the positive x-axis is
![]()
As such, vectors are really parametric functions. Therefore, the rate of change of a vector is determined determining the rates of change for its components:
![]()